Pourquoi Les Traders à 500 Milliards Maîtrisent le Risk of Ruin (Et Pas Vous)

Près de 90 % des traders particuliers perdent de l’argent sur les marchés. La raison souvent invoquée ? Un manque de discipline. Pourtant, cette explication passe à côté du véritable enjeu. Ce qui fait la différence entre un trader qui abandonne après quelques pertes et celui qui construit une stratégie rentable sur le long terme, ce n’est pas la discipline — c’est la conviction.

La conviction dans une stratégie de trading algorithmique ne naît pas du hasard. Elle se construit sur des fondations solides : des backtests rigoureux, une compréhension profonde des mécanismes de profit, et surtout, une gestion de risque scientifique. Car rester dans le jeu sur le long terme, c’est accepter l’incertitude tout en la mesurant avec précision.

Aujourd’hui, nous allons explorer l’un des outils les plus fondamental pour développer cette conviction : le Risk of Ruin (risque de ruine), une méthodologie qui permet d’estimer la probabilité de subir des pertes importantes et d’anticiper les pires drawdowns possibles.

Gestion de Risque en Trading : Au-delà des Règles Simplistes

La gestion de risque représente le pilier central du trading rentable. Jeff Yass, fondateur de Susquehanna Capital — un fond avec plus de 500 milliards de dollars sous gestion — le résume ainsi : “Même si vous avez une paire d’as, vous ne miseriez jamais 100 % de votre argent. Parce que 20 % du temps, vous allez le perdre. La clé n’est pas de gagner un coup, c’est de rester à la table.”

Mais comment appliquer concrètement ce principe de survie à long terme ? Les “gourous” du trading proposent des règles universelles : ne jamais risquer plus de 2 % par trade, toujours viser un risk-reward ratio de 3:1, placer systématiquement des stop-loss. Des formules fixes, appliquées aveuglément quel que soit le contexte.

Alors que pour les professionnels expérimentés et les hedge funds, la gestion de risque doit être statistique et plus approfondie. Elle ne peut ignorer la corrélation entre positions, doit calculer la Value at Risk en temps réel, et ajuster l'exposition selon le contexte global. C'est précisément dans ce cadre statistique que le Risk of Ruin s'installe comme un outil clé.

Le Risk of Ruin : Mesurer l’Incertitude

Stratégie Trix : Exemple de Backtest et Analyse de Drawdown

Prenons un exemple concret pour illustrer l’application du Risk of Ruin : la stratégie Trix, basée sur l’indicateur technique du même nom, que nous avons développée, optimisée et mise en production sur plusieurs vidéos de la chaîne, toujours en open source (https://www.youtube.com/watch?v=A7z–mZx4AY, https://www.youtube.com/watch?v=9GqvJoJEOVs).

Entre 2021 et fin octobre 2025, voici les performances de cette stratégie en backtest :

• Performance totale : +681 % (contre +284 % pour le Bitcoin sur la même période)
• Drawdown maximum observé : -30 % (contre environ -80 % pour le Bitcoin)
• Nombre de trades : 5100 (échantillon statistiquement robuste)
• Levier utilisé : ajustable selon le profil de risque

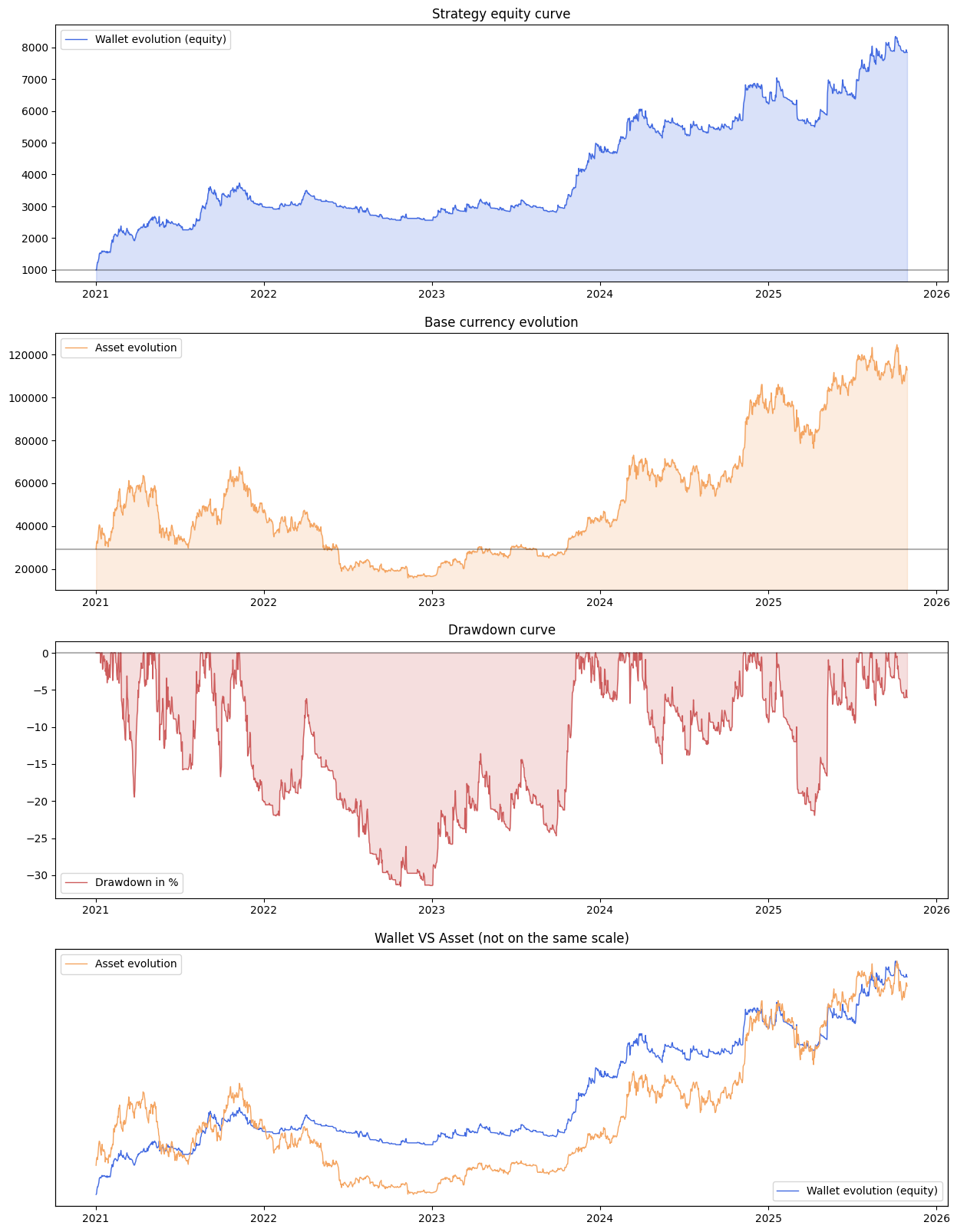
Sur le graphique ci-dessus, on observe la courbe de croissance du capital sur presque 4 années. La performance est largement supérieure au Bitcoin, avec une volatilité maîtrisée. Le drawdown reste important, de 30 % et se manifeste à plusieurs reprises, notamment lors des phases de consolidation du marché crypto.

Mais voici la question cruciale : ce drawdown de -30 % observé dans le passé représente-t-il vraiment le pire scénario possible ?

Si demain la stratégie subit une perte de 40 %, faut-il tout remettre en question ? Ou est-ce statistiquement plausible compte tenu de la nature probabiliste des marchés ? Si on atteint -50 %, est-ce un signal d’alerte réel ou une variation normale ?

Sans méthode pour répondre à ces questions, impossible de développer une conviction solide. À la première grosse perte, le doute s’installe, et même une stratégie gagnante sur le long terme sera abandonnée prématurément.

C’est exactement ce que le Risk of Ruin permet de calculer.

Calculer le Risk of Ruin : Méthodologie Monte Carlo

Le Risk of Ruin estime la probabilité d’atteindre ou dépasser un certain drawdown au cours d’une période future. La méthodologie repose sur des simulations de Monte Carlo :

1. On part des 5100 trades historiques de la stratégie Trix
2. On génère 10 000 trajectoires futures en mélangeant aléatoirement l’ordre des trades (avec remise)
3. Pour chaque trajectoire, on extrait le pire drawdown (Maximum Drawdown ou MDD)
4. On obtient ainsi une distribution statistique des drawdowns possibles
5. On calcule pour chaque seuil (10 %, 20 %, 30 %…) la probabilité de l’atteindre

Pour tester la robustesse, on simule trois scénarios en ajoutant du "bruit" aux trades historiques (variation aléatoire pour simuler une dégradation potentielle des performances futures).

Sur le graphique ci-dessus, on observe trois courbes :

• Courbe bleue (noise=0.0) : simulation pure des trades historiques sans ajout de variabilité — scénario optimiste
• Courbe orange (noise=0.5) : ajout d'un bruit modéré — scénario réaliste recommandé
• Courbe verte (noise=1.0) : scénario pessimiste avec bruit standard

L'axe horizontal représente le drawdown maximum (de 5 % à 95 %), l'axe vertical la probabilité de l'atteindre (de 0 à 1, soit 0 % à 100 %).

On observe ainsi pour la stratégie Trix (courbe orange, scénario réaliste) :

• 80 % de probabilité de subir au moins 20 % de drawdown au cours des trois prochaines années
• 40-50 % de probabilité d'atteindre 30 % de drawdown
• 15-20 % de probabilité d'atteindre 40 % de drawdown
• Moins de 5 % de probabilité d'atteindre 50 % de drawdown

Cette information est cruciale pour calibrer ses attentes. Elle permet de distinguer une variation normale d'un dysfonctionnement réel de la stratégie. Si la stratégie Trix subit 35 % de drawdown, ce n'est pas nécessairement un signal d'arrêt — cela reste dans l'enveloppe statistique attendue (environ 25-30 % de probabilité selon le scénario).

À l'inverse, si on atteint 60 % de drawdown, c'est un événement très improbable (moins de 2 % de chances) qui pourrait signaler un problème structurel : changement de régime de marché, bug dans le code, slippage non anticipé, etc.

Enfin, si les résultats révèlent des probabilités de drawdown que vous ne seriez pas en mesure de tolérer psychologiquement ou financièrement, c'est le signal qu'il faut réviser l'optimisation — voire la stratégie elle-même — avant de la mettre en production avec de l'argent réel.

Implémenter le Risk of Ruin en Python

Voici la fonction Python que nous avons utilisée pour calculer le Risk of Ruin. Elle peut s’appliquer à n’importe quelle stratégie de trading disposant d’un historique de trades :

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from typing import Optional, Tuple, Dict

def risk_of_ruin_curve(
    daily_return: pd.Series,
    n_paths: int = 10000,
    path_length: int = 2*365,
    noise_std: float = 1.0,                      # défaut à 1.0
    thresholds: Optional[np.ndarray] = np.arange(0.05, 1.0, 0.05),     # si None => tous les 10%
    resample_with_replacement: bool = True,
    seed: Optional[int] = None,
) -> Tuple[pd.DataFrame, Dict[str, np.ndarray]]:
    """
    Simule des trajectoires, calcule le MDD de chacune, puis estime
    P(MDD ≥ seuil) pour des seuils échantillonnés tous les 10 %.
    Trace 3 courbes: bruit=0.0, bruit=0.5 et bruit=noise_std (défaut 1.0).
    """
    rng = np.random.default_rng(seed)

    r = pd.Series(daily_return).dropna().astype(float).values
    if r.size == 0:
        raise ValueError("daily_return est vide après dropna().")

    hist_std = np.std(r, ddof=1)
    n_hist = r.size

    # Seuils tous les 10% par défaut (0.1 à 0.9)
    if thresholds is None:
        thresholds = np.arange(0.1, 1.0, 0.1)
    thresholds = np.asarray(thresholds, dtype=float)

    def simulate_mdd(noise_mult: float) -> np.ndarray:
        """Retourne un vecteur (n_paths,) des MDD simulés pour un multiple d'écart-type donné."""
        noise_scale = float(noise_mult) * hist_std
        mdd_vals = np.empty(n_paths, dtype=float)

        for i in range(n_paths):
            if not resample_with_replacement and path_length <= n_hist:
                idx = rng.choice(n_hist, size=path_length, replace=False)
            else:
                idx = rng.choice(n_hist, size=path_length, replace=True)

            path = r[idx].copy()
            if noise_scale > 0.0:
                path += rng.normal(0.0, noise_scale, size=path_length)

            equity = np.cumprod(1.0 + path)
            running_max = np.maximum.accumulate(equity)
            drawdown = (equity / running_max) - 1.0
            mdd_vals[i] = -np.min(drawdown)  # MDD positif (ex: 0.23 = 23%)

        return mdd_vals

    # Scénarios de bruit
    scenarios = {
        "noise=0.0": 0.0,
        "noise=0.5": 0.5,
        f"noise={noise_std:g}": noise_std,
    }

    # Simulations + courbes
    risks_by_scenario = {}
    mdd_by_scenario: Dict[str, np.ndarray] = {}

    plt.figure(figsize=(12, 6))
    for label, mult in scenarios.items():
        mdd_vals = simulate_mdd(mult)
        mdd_by_scenario[label] = mdd_vals
        risks = (mdd_vals[:, None] >= thresholds[None, :]).mean(axis=0)
        risks_by_scenario[label] = risks
        plt.plot(thresholds, risks, marker="o", label=label)

    plt.xlabel("Drawdown max")
    plt.ylabel("Risk of ruin")
    plt.title("Risk of ruin vs. max drawdown")
    plt.grid(True, alpha=0.3)
    plt.legend()
    plt.show()

Comment utiliser cette fonction ?

Étape 1 : Calculer les daily returns depuis votre backtest

Peu importe votre framework de backtesting, vous devez extraire l’évolution de votre capital jour par jour. Voici comment calculer les returns journaliers :

# Supposons que vous ayez une série de valeurs de portefeuille par jour
equity_curve = pd.Series([1000, 1020, 1015, 1030, 1025, ...])  # Valeurs quotidiennes

# Calculer les returns journaliers (variation en pourcentage)
daily_returns = equity_curve.pct_change().dropna()

# Exemple de résultat :
# [0.02, -0.0049, 0.0148, -0.0049, ...]  # +2%, -0.49%, +1.48%, etc.

Si votre backtest génère des trades avec timestamps mais pas de valeur quotidienne, vous devrez reconstruire l’equity curve quotidienne en interpolant entre les trades.

Étape 2 : Appeler la fonction

# Appel avec paramètres par défaut (recommandé pour débuter)
results_df, mdd_distributions = risk_of_ruin_curve(daily_returns)

# Appel avec personnalisation
results_df, mdd_distributions = risk_of_ruin_curve(
    daily_return=daily_returns,
    n_paths=10000,           # Nombre de simulations Monte Carlo
    path_length=3*365,       # Horizon : 3 ans (en jours de trading)
    noise_std=1.0,           # Écart-type du bruit ajouté (scénario pessimiste)
    thresholds=np.arange(0.05, 0.95, 0.05),  # Seuils de DD de 5% à 95% par pas de 5%
    seed=42                  # Pour reproductibilité
)

Paramètres détaillés :

• daily_return : Series Pandas des returns journaliers (obligatoire)
• n_paths : Nombre de trajectoires simulées (défaut 10000, augmenter pour plus de précision)
• path_length : Horizon de simulation en jours (défaut 2×365 = 2 ans)
• noise_std : Multiplicateur de bruit (0.0 = aucun, 0.5 = modéré, 1.0 = standard)
• thresholds : Array des seuils de drawdown à évaluer (de 0.0 à 1.0)
• resample_with_replacement : Si True, échantillonnage avec remise (recommandé)
• seed : Graine aléatoire pour reproductibilité

Étape 3 : Interpréter les résultats

La fonction retourne un DataFrame et un dictionnaire :

# results_df contient les probabilités pour chaque scénarioprint(results_df.head())
#          noise=0.0  noise=0.5  noise=1.0# 0.05      0.98       0.99       0.99# 0.10      0.92       0.95       0.97# 0.15      0.78       0.85       0.91# ...# Pour savoir : quelle probabilité d'atteindre 30% de DD avec bruit modéré ?prob_30_percent = results_df.loc[0.30, "noise=0.5"]
print(f"Probabilité d'atteindre 30% DD : {prob_30_percent*100:.1f}%")

À partir de là, vous pouvez faire vos propres analyses et les plots que vous souhaitez.

Conclusion : Vers une Conviction Statistique en Trading

Le Risk of Ruin n’est qu’un outil parmi d’autres dans l’arsenal de la gestion de risque statistique, mais c’est un outil décisif. Au lieu de découvrir un drawdown de 35 % avec panique, on peut anticiper : “J’ai environ 20-25 % de chances de vivre ça dans les 3 prochaines années. Si ça arrive, c’est normal, je continue.” Cette acceptation éclairée de la variabilité transforme complètement la perception du risque.

Si vous ne l’avez pas encore vu, le code ci-dessus etait le code promis dans notre dernière vidéo sur le poker et le trading algorithmique :

Cette vidéo explore d’autres dimensions clés : pourquoi Susquehanna Capital — avec ses 500 milliards sous gestion — oblige tous ses traders à devenir experts au poker, comment identifier son edge (inefficiences de marché vs primes de risque), et comment la théorie des jeux s’applique concrètement aux marchés financiers.

Bon et bien… Maintenant que vous connaissez votre Risk of Ruin, il ne reste plus qu’à l’éviter ;) !